Calculate Max Lift Drag Ratio

Measure out of aerodynamic efficiency

In aerodynamics, the lift-to-drag ratio (or L/D ratio) is the elevator generated by an aerodynamic body such equally an aerofoil or aircraft, divided past the aerodynamic drag caused by moving through air. It describes the aerodynamic efficiency under given flight conditions. The 50/D ratio for any given body volition vary according to these flight conditions.

For an aerofoil fly or powered aircraft, the 50/D is specified when in straight and level flight. For a glider information technology determines the glide ratio, of distance travelled confronting loss of height.

The term is calculated for any item airspeed past measuring the lift generated, then dividing by the drag at that speed. These vary with speed, so the results are typically plotted on a ii-dimensional graph. In almost all cases the graph forms a U-shape, due to the two master components of drag. The L/D may be calculated using computational fluid dynamics or computer simulation. It is measured empirically by testing in a wind tunnel or in free flight test.^[1] ^[2] ^[3]

The L/D ratio is affected past both the form drag of the body and by the induced drag associated with creating a lifting force. It depends principally on the lift and drag coefficients, bending of attack to the airflow and the wing aspect ratio.

The L/D ratio is inversely proportional to the energy required for a given flightpath, so that doubling the L/D ratio will crave simply one-half of the energy for the same distance travelled. This results directly in meliorate fuel economic system.

Lift and drag [edit]

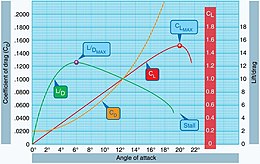
Drag vs Speed. Fifty/DMAX occurs at minimum Total Drag (eastward.g. Parasite plus Induced)

Polar curve showing glide angle for the all-time glide speed (best L/D). It is the flattest possible glide angle through calm air, which volition maximize the distance flown. This airspeed (vertical line) corresponds to the tangent signal of a line starting from the origin of the graph. A glider flying faster or slower than this airspeed will encompass less distance before landing.^[4] ^[v]

Lift is created whenever an asymmetric body travels through a viscous fluid such equally air. The asymmetry of an aerofoil is typically introduced by designing-in camber and/or setting it at an angle of attack to the airflow. The lift then increases as the foursquare of the airspeed.

Whenever an aerodynamic body generates lift, this also creates induced, or lift-induced drag. At low speeds an aircraft has to generate lift with a college angle of attack, which results in a greater induced drag. This term dominates the low-speed side of the graph of elevator versus velocity.

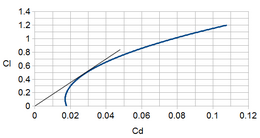
Drag curve for lite aircraft. The tangent gives the maximum $L/D$ signal.

Form elevate is acquired by motion of the body through air. This type of elevate, known also every bit air resistance or profile drag varies with the square of speed (see drag equation). For this reason contour drag is more pronounced at greater speeds, forming the right side of the lift/velocity graph'south U shape. Profile drag is lowered primarily by streamlining and reducing cross section.

The total drag on any aerodynamic body thus has two components, induced drag and class drag.

Lift and drag coefficients [edit]

The rates of change of lift and drag with bending of set on (AoA) are chosen respectively the lift and drag coefficients C₅₀ and C_D. The varying ratio of lift to elevate with AoA is oft plotted in terms of these coefficients.

For any given value of lift, the AoA varies with speed. Graphs of C_Fifty and C_D vs. speed are referred to equally drag curves. Speed is evidence increasing from left to correct. The elevator/drag ratio is given past the slope from the origin to some betoken on the curve and so the maximum L/D ratio does not occur at the indicate of least elevate, the leftmost betoken. Instead it occurs at a slightly greater speed. Designers will typically select a wing blueprint which produces an 50/D peak at the chosen cruising speed for a powered fixed-wing aircraft, thereby maximizing economy. Like all things in aeronautical engineering, the lift-to-drag ratio is not the only consideration for fly design. Performance at a high angle of attack and a gentle stall are also important.

Glide ratio [edit]

As the aircraft fuselage and control surfaces volition also add drag and maybe some lift, it is fair to consider the 50/D of the aircraft every bit a whole. As it turns out, the glide ratio, which is the ratio of an (unpowered) shipping'southward forrad movement to its descent, is (when flown at constant speed) numerically equal to the aircraft's L/D. This is particularly of involvement in the design and operation of high performance sailplanes, which can take glide ratios almost 60 to 1 (lx units of distance forward for each unit of measurement of descent) in the best cases, just with 30:1 being considered good performance for general recreational use. Achieving a glider'south best 50/D in practice requires precise control of airspeed and smooth and restrained operation of the controls to reduce elevate from deflected control surfaces. In nothing wind conditions, 50/D will equal distance traveled divided by distance lost. Achieving the maximum distance for altitude lost in air current conditions requires further modification of the best airspeed, every bit does alternating cruising and thermaling. To achieve high speed across land, glider pilots anticipating strong thermals often load their gliders (sailplanes) with h2o ballast: the increased fly loading ways optimum glide ratio at greater airspeed, but at the cost of climbing more slowly in thermals. Equally noted below, the maximum L/D is non dependent on weight or wing loading, but with greater wing loading the maximum L/D occurs at a faster airspeed. Also, the faster airspeed means the shipping will wing at greater Reynolds number and this volition usually bring about a lower zero-lift drag coefficient.

Theory [edit]

Subsonic [edit]

Mathematically, the maximum elevator-to-drag ratio tin can exist estimated as:

(50/D)_{\max }={\frac {one}{2}}{\sqrt {\frac {\pi \varepsilon AR}{C_{D,0}}}},

^[6]

where AR is the aspect ratio, $\varepsilon$ the span efficiency cistron, a number less than but shut to unity for long, straight edged wings, and $C_{D,0}$ the zero-lift drag coefficient.

Most chiefly, the maximum lift-to-drag ratio is independent of the weight of the aircraft, the expanse of the fly, or the fly loading.

It tin can be shown that two main drivers of maximum elevator-to-drag ratio for a fixed wing aircraft are wingspan and total wetted area. One method for estimating the zero-elevator elevate coefficient of an aircraft is the equivalent skin-friction method. For a well designed aircraft, zero-lift drag (or parasite drag) is more often than not made up of peel friction drag plus a small percentage of pressure drag caused past period separation. The method uses the equation:

C_{D,0}=C_{\text{iron}}{\frac {S_{\text{wet}}}{S_{\text{ref}}}},

^[seven]

where $C_{\text{fe}}$ is the equivalent skin friction coefficient, $S_{\text{wet}}$ is the wetted area and $S_{\text{ref}}$ is the fly reference area. The equivalent pare friction coefficient accounts for both separation drag and peel friction drag and is a fairly consistent value for aircraft types of the same class. Substituting this into the equation for maximum lift-to-drag ratio, along with the equation for aspect ratio ( $b^{2}/S_{\text{ref}}$ ), yields the equation:

(L/D)_{\max }={\frac {1}{2}}{\sqrt {{\frac {\pi \varepsilon }{C_{\text{fe}}}}{\frac {b^{2}}{S_{\text{moisture}}}}}}

where b is wingspan. The term $b^{ii}/S_{\text{moisture}}$ is known as the wetted aspect ratio. The equation demonstrates the importance of wetted attribute ratio in achieving an aerodynamically efficient blueprint.

Supersonic [edit]

At very bully speeds, lift to drag ratios tend to exist lower. Concorde had a lift/drag ratio of about 7 at Mach 2, whereas a 747 is nearly 17 at almost mach 0.85.

Dietrich Küchemann adult an empirical human relationship for predicting 50/D ratio for high Mach:^[eight]

L/D_{\max }={\frac {four(Thou+3)}{M}}

where M is the Mach number. Windtunnel tests have shown this to be approximately accurate.

Examples of 50/D ratios [edit]

The eta has the all-time glide ratio for a sailplane

House sparrow: iv:1
Herring dupe x:1
Mutual tern 12:1
Albatross 20:1
Wright Flyer 8.3:1
Boeing 747 in cruise 17.7:ane.^[9]
Cruising Airbus A380 twenty:one^[ten]
Concorde at takeoff and landing 4:1, increasing to 12:i at Mach 0.95 and vii.5:1 at Mach 2^[11]
Helicopter at 100 kn (190 km/h) four.v:one^[12]
Cessna 172 gliding x.ix:1^[13]
Cruising Lockheed U-2 25.6:i^[14]
Rutan Voyager 27:1
Virgin Atlantic GlobalFlyer 37:one^[15]

Computed aerodynamic characteristics^[16]
Jetliner	cruise Fifty/D	Get-go flight
L1011-100	xiv.5	November 16, 1970
DC-10-forty	13.8	Aug 29, 1970
A300-600	15.ii	Oct 28, 1972
Dr.-11	16.1	January x, 1990
B767-200ER	16.1	Sep 26, 1981
A310-300	fifteen.3	April three, 1982
B747-200	xv.3	Feb ix, 1969
B747-400	15.5	Apr 29, 1988
B757-200	15.0	Feb 19, 1982
A320-200	16.3	February 22, 1987
A310-300	18.1	Nov 2, 1992
A340-200	19.ii	Apr ane, 1992
A340-300	19.1	Oct 25, 1991
B777-200	xix.3	Jun 12, 1994

See as well [edit]

Gravity elevate rockets tin have an effective elevator to drag ratio while maintaining altitude.
Inductrack maglev
Lift coefficient
Range (aeronautics) range depends on the elevator/drag ratio.
Thrust specific fuel consumption the lift to elevate determines the required thrust to maintain altitude (given the aircraft weight), and the SFC permits calculation of the fuel burn rate.
Thrust-to-weight ratio

References [edit]

^[13]

^ Accurate adding of aerodynamic coefficients of parafoil airdrop system based on computational fluid dynamic Wannan Wu , Qinglin Sun, Shuzhen Luo, Mingwei Sun, Zengqiang Chen and Hao Dominicus: International Journal of Advanced Robotic Systems
^ Validation of software for the adding of aerodynamic coefficientsaerodynamic coefficientsaerodynamic coefficientsaerodynamic coefficients Ramón López Pereira, Linköpings Universitet
^ In-flight Lift and Drag Estimation of an Unmanned Propeller-Driven Aircraft Dominique Paul Bergmann, January Denzel, Ole Pfeifle, Stefan Notter, Walter Fichter and Andreas Strohmayer
^ Wander, Bob (2003). Glider Polars and Speed-To-Fly...Made Like shooting fish in a barrel!. Minneapolis: Bob Wander'southward Soaring Books & Supplies. p. 7-10.
^ Glider Flying Handbook, FAA-H-8083-13. U.S. Section of Transportation, FAA. 2003. p. five-half dozen to 5-nine. ISBN9780160514197.
^ Loftin, LK Jr. "Quest for operation: The development of modernistic aircraft. NASA SP-468". Retrieved 2006-04-22 .
^ Raymer, Daniel (2012). Aircraft Design: A Conceptual Approach (fifth ed.). New York: AIAA.
^ Aerospaceweb.org Hypersonic Vehicle Design
^ Antonio Filippone. "Elevator-to-Drag Ratios". Advanced topics in aerodynamics. Archived from the original on March 28, 2008.
^ Cumpsty, Nicholas (2003). Jet Propulsion. Cambridge University Press. p. four.
^ Christopher Orlebar (1997). The Concorde Story. Osprey Publishing. p. 116. ISBN9781855326675. ^{[ permanent dead link ]}
^ Leishman, J. Gordon (24 April 2006). Principles of helicopter aerodynamics. Cambridge University Printing. p. 230. ISBN0521858607. The maximum elevator-to-drag ratio of the complete helicopter is about 4.v
^ ^a ^b Cessna Skyhawk II Performance Assessment http://temporal.com.au/c172.pdf
^
U2 Developments transcript. Primal Intelligence Agency. 1960. Archived from the original on 2022-06-nineteen. Retrieved 2016-03-05 – via YouTube.
- "U2 Developments". Central Intelligence Agency. June iv, 2013. Archived from the original on 2013-08-16.
^ David Noland (Feb 2005). "The Ultimate Solo". Pop Mechanics.
^ Rodrigo Martínez-Val; et al. (January 2005). "Historical evolution of air send productivity and efficiency". 43rd AIAA Aerospace Sciences Meeting and Exhibit. doi:10.2514/6.2005-121. ^{[ permanent dead link ]}

External links [edit]

Lift-to-drag ratio calculator